Metoda gradientu prostego

Ten artykuł od 2020-10 zawiera treści, przy których brakuje odnośników do źródeł.

Należy dodać przypisy do treści niemających odnośników do źródeł. Dodanie listy źródeł bibliograficznych jest problematyczne, ponieważ nie wiadomo, które treści one uźródławiają.
Sprawdź w źródłach: Encyklopedia PWN • Google Books • Google Scholar • Federacja Bibliotek Cyfrowych • BazHum • BazTech • RCIN • Internet Archive (texts / inlibrary)
Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu.
Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

Metoda gradientu prostego – algorytm numeryczny mający na celu znalezienie minimum lokalnego zadanej funkcji celu.

Jest to jedna z prostszych metod optymalizacji. Przykładami innych metod są metoda najszybszego spadku, czy metoda Newtona.

Metoda gradientu prostego jest iteracyjnym algorytmem wyszukiwania minimum zadanej funkcji celu ${\displaystyle f{:}}$

${\displaystyle f\colon D\mapsto \mathbb {R} ,}$

gdzie ${\displaystyle D\subset \mathbb {R} ^{n}.}$

Założenia dla metody są następujące:

• ${\displaystyle f\in \mathrm {C} ^{1}}$ (funkcja jest ciągła i różniczkowalna),
• ${\displaystyle f}$ jest ściśle wypukła w badanej dziedzinie.

Na samym początku algorytmu wybierany jest punkt startowy ${\displaystyle \mathbf {x_{0}} \in D.}$ W punkcie tym obliczany jest kierunek poszukiwań ${\displaystyle \mathbf {d_{k}} \in D.}$ Punkt w następnym kroku obliczany jest według wzoru:

${\displaystyle \mathbf {x_{k+1}} =\mathbf {x_{k}} +\alpha _{k}\mathbf {d_{k}} ,}$

jeśli obliczony punkt nie spełni warunku stopu algorytmu, całe postępowanie jest powtarzane.

Kierunkiem poszukiwań w metodzie gradientu prostego jest antygradient funkcji celu ${\displaystyle -\nabla f(\mathbf {x_{k}} ).}$

Współczynnik ${\displaystyle \alpha _{k}}$ jest współczynnikiem długości kolejnych kroków. W wielu przypadkach przyjmuje się stałe niewielkie wartości:

${\displaystyle \alpha _{k}=\alpha ={\textrm {const}}.}$

Jeśli ${\displaystyle f}$ jest funkcją kwadratową o dodatnio określonym hesjanie ${\displaystyle H}$ to można przyjąć:

${\displaystyle 0<\alpha <{\frac {1}{\lambda }}.}$

gdzie ${\displaystyle \lambda }$ jest największą wartością własną macierzy ${\displaystyle H.}$

Współczynnik ${\displaystyle \alpha _{k}}$ może również dynamicznie zmieniać się podczas procesu szukania minimum. Kolejne kroki w algorytmie powinny być wybierane tak aby:

${\displaystyle f(\mathbf {x_{0}} )>\dots >f(\mathbf {x_{k}} )>f(\mathbf {x_{k+1}} ).}$

Jeżeli warunek ten nie jest w danym kroku spełniony, to należy powtórzyć krok z mniejszą wartością ${\displaystyle \alpha _{k}.}$

Algorytm ogólnie można zapisać:

1. Wybierz punkt startowy ${\displaystyle \mathbf {x_{0}} .}$
2. ${\displaystyle \mathbf {x_{k+1}} =\mathbf {x_{k}} -\alpha _{k}\nabla f(\mathbf {x_{k}} ).}$
3. Sprawdź kryterium stopu, jeśli jest spełniony to STOP.
4. Jeżeli ${\displaystyle f(\mathbf {x_{k+1}} )\geqslant f(\mathbf {x_{k}} )}$ to zmniejsz wartość ${\displaystyle \alpha _{k}}$ i powtórz punkt 2 dla kroku ${\displaystyle k}$-tego.
5. Powtórz punkt 2 dla następnego kroku ${\displaystyle (k+1).}$

W celu określenia, czy punkt w danym kroku dostatecznie dobrze przybliża minimum funkcji celu w metodzie gradientu prostego, można użyć następujących kryteriów stopu (dla zadanej precyzji ${\displaystyle \epsilon }$ oraz normy ${\displaystyle \|{\cdot }\|}$):

${\displaystyle \|\nabla f(\mathbf {x_{k}} )\|\leqslant \epsilon ,\quad {}}$ (test stacjonarności)

${\displaystyle \|\mathbf {x_{k+1}} -\mathbf {x_{k}} \|\leqslant \epsilon .}$

Metoda gradientu prostego jest metodą o zbieżności liniowej. Oznacza to, iż przy spełnieniu założeń metody, odległości pomiędzy kolejnymi przybliżeniami a minimum funkcji ${\displaystyle \mathbf {x} ^{*}}$ maleją liniowo:

${\displaystyle \|\mathbf {x} ^{*}-\mathbf {x_{k+1}} \|\leqslant c\|\mathbf {x} ^{*}-\mathbf {x_{k}} \|.}$

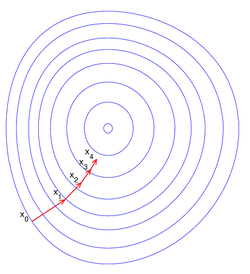
Na poniższych rysunkach zilustrowane zostały kolejne kroki metody gradientu prostego dla funkcji:

${\displaystyle F(x,y)=\sin \left({\frac {1}{2}}x^{2}-{\frac {1}{4}}y^{2}+3\right)\cos(2x+1-e^{y}).}$

• metoda najszybszego spadku
• metoda Newtona
• metoda złotego podziału
• optymalizacja

• Fortuna Z., Macukow B., Wąsowski J.: Metody numeryczne, Wydawnictwa Naukowo-Techniczne, 2006.* Stachurski A., Wierzbicki A.: Podstawy optymalizacji, Oficyna Wydawnicza Politechniki Warszawskiej, 1999.

• https://web.archive.org/web/20170815181749/http://www.isep.pw.edu.pl/~ambor/Pomoce/gradientowe.htm