Trapez

Ten artykuł dotyczy pojęcia geometrycznego. Zobacz też: inne znaczenia tego słowa.

Zobacz hasło trapez w Wikisłowniku

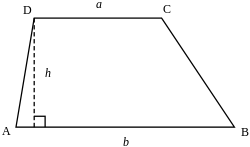
Trapez – czworokąt z przynajmniej jedną parą równoległych boków^[1]. Czasem zakłada się dokładnie jedną taką parę, przy takiej definicji równoległobok nie byłby trapezem^[2][1].

Boki równoległe nazywa się podstawami, pozostałe ramionami, a odcinek łączący podstawy i prostopadły do nich – oraz jego długość, czyli odległość między podstawami – wysokością trapezu^[1]. Wszystkie trapezy są wypukłe^{[potrzebny przypis]}.

Dla dowolnego trapezu suma miar kątów wewnętrznych leżących przy tym samym ramieniu jest równa 180°^[1]. Jest tak, ponieważ ramię trapezu jest sieczną (transwersalą) podstaw – zob. kąty wyznaczane przez proste; kąty przy tym samym ramieniu to para kątów jednostronnych wewnętrznych.

Jeśli ${\displaystyle P}$ oznacza punkt przecięcia przekątnych, to^{[potrzebny przypis]}:

• trójkąty ${\displaystyle ADP}$ i ${\displaystyle BCP}$ mają równe pola^[a];
• trójkąty ${\displaystyle ABP}$ i ${\displaystyle CDP}$ są podobne, co wynika wprost z twierdzenia Talesa.

Jest to iloczyn wysokości i średniej arytmetycznej długości podstaw – połowy ich sumy^[1][3]:

${\displaystyle S={\frac {a+b}{2}}\ h}$

gdzie ${\displaystyle a,b}$ to długości podstaw, a ${\displaystyle h}$ to jego wysokość.

Inny wzór na pole powierzchni trapezu zawiera długości wszystkich boków (podstaw i ramion)^{[potrzebny przypis]}:

${\displaystyle S={\frac {1}{4}}{\frac {a+b}{|a-b|}}\ {\sqrt {|a-b|+c+d}}\ {\sqrt {|a-b|+c-d}}\ {\sqrt {|a-b|-c+d}}\ {\sqrt {-|a-b|+c+d}}}$

gdzie ${\displaystyle a\neq b}$ to długości podstaw, ${\displaystyle c,d}$ – długości ramion^[b].

Trapez o ramionach równej długości^[1]. Jeśli taki trapez nie jest równoległobokiem niebędącym prostokątem, to ma on oś symetrii: przechodzącą przez środki podstaw ich wspólną symetralną. W tym przypadku kąty między ramionami a daną podstawą są równe, a kąty przeciwległe sumują się do 180°; stąd można go wtedy wpisać w okrąg.

Pole powierzchni trapezu równoramiennego można wyrazić wzorem^{[potrzebny przypis]}

${\displaystyle S={\frac {g^{2}}{2}}\ \sin \varphi ,}$

gdzie ${\displaystyle g}$ oznacza długość przekątnej trapezu (obie mają równą długość), a ${\displaystyle \varphi }$ to kąt między przekątnymi trapezu.

Trapez, którego kąt wewnętrzny jest prosty, tj. ma miarę 90°^[1]. Ramię trapezu jako sieczna (transwersala) podstaw (zob. kąty wyznaczane przez proste) przecina je obie pod kątem prostym, dlatego trapez prostokątny musi mieć co najmniej dwa kąty proste. Szczególnym przypadkiem trapezu prostokątnego jest prostokąt – ma on cztery kąty wewnętrzne proste.

• deltoid
• prostokąt
• równoległobok
• trapezoid

• Artykuły na Zintegrowanej Platformie Edukacyjnej, zpe.gov.pl :
  • Paweł Dziuba, Trapez i jego własności;
  • Bogdan Staruch, Odcinek łączący środki ramion trapezu;
  • Tomasz Paszek, Pole trapezu.
• JoannaJ. Jaszuńska JoannaJ., Średnie w trapezie, „Delta”, październik 2005, ISSN 0137-3005  .
• Dowody wzoru na pole trapezu, zadania.info .